Support vector machine (SVM) is a powerful supervised machine learning algorithm used for classification and regression tasks.
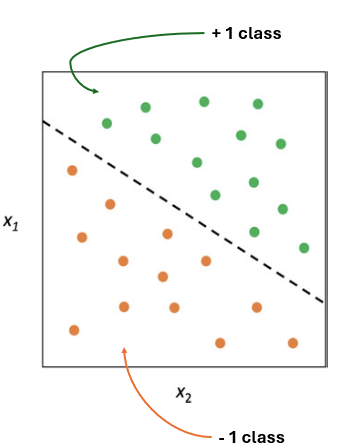
The objective of SVM is to find the optimal hyperplane that separates the datapoints into different classes or categories in the future space while maximixing the margin between the classes.
SVM is effective for binary classification problems but can be extended to handle multi-class classification and regression tasks.
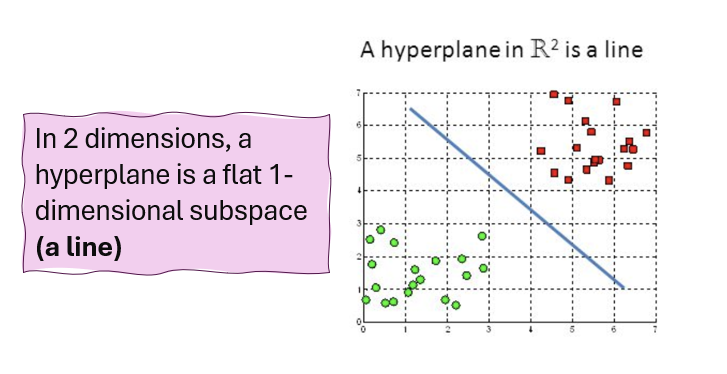
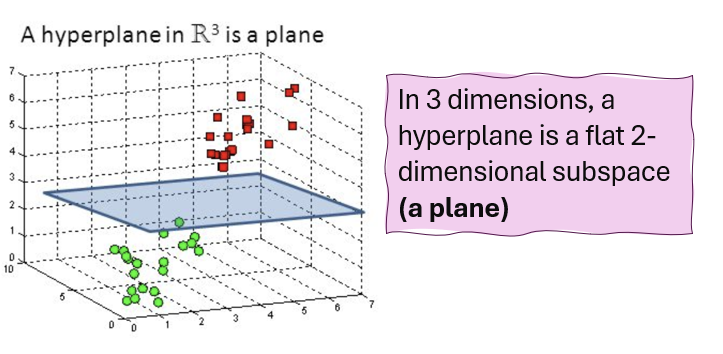
Hyperplane
A flat affine subspace of dimension \(p-1\). A hyperplane is a decision boundary that separates the feature space into different regions corresponding to different classes.
In \(p>3\) dimensions, it can be hard to visualise a hyperplane, but the notion of a \(p-1\) -dimensional flat subspace still applies.
The mathematical definition of a hyperplane in \(p\)-dimensions:
\[
h(x)= \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+...+\beta_{p}X_{p}=0
\]
Defines a \(p\)-dimensional hyperplane for a point \[X=(X_{1},X_{2},..,X_{1})^T\] in \(p\)-dimensional space.
Suppose that \(X\) does not satisfy the equation but:-
\(y_{i} \times h(X)>0\) , then \(X\) lies on \(+1\) class (green), if \(y_{i} \times h(X)<0\) , then \(X\) lies on \(+1\) class (orange)
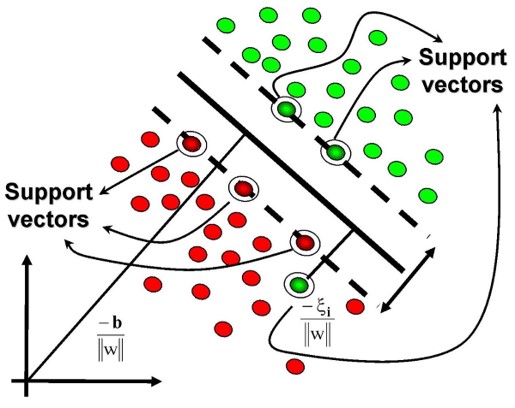
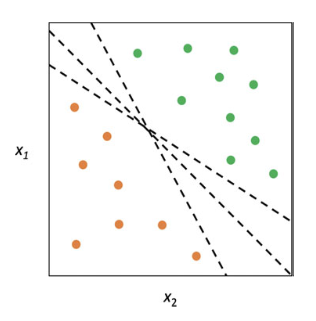
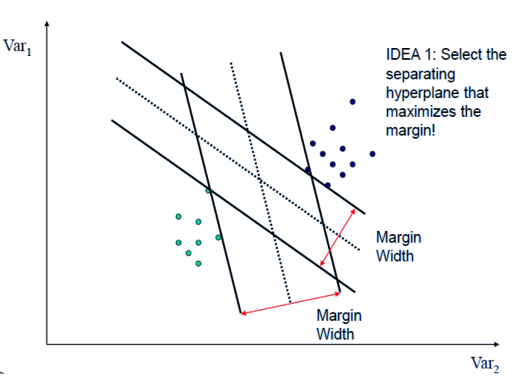
The separating hyperplane cannot be unique. One can define many separating hyperplane within the same dataset. To choose the “best” one (Maximal Margin Hyperplane), We can compute the perpendicular distance from each training observation or retain the smallest distance (called “margin”).
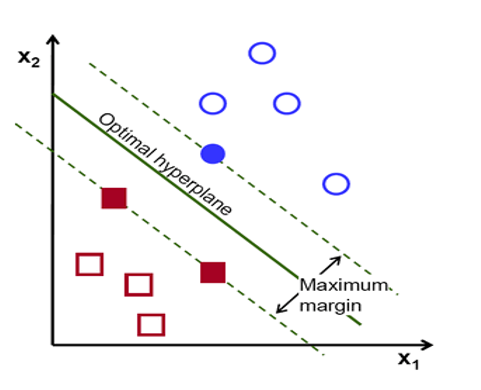
Maximal Margin
Maximal margin is the distance between the hyperplane and the nearest data point (support vector) from each class. The optimal hyperplane in SVM is the one that maximizes this margin, providing the largest separation or margin between the class.
Maximal Margin is the separating hyperplane for which the margin is largest. It is the hyperplane that has the largest minimum distance to the training observations.
The maximal margin hyperplane is determined by searching the largest minimal distance between observation and the separating hyperplane. The solution of maximal margin hyperplane :
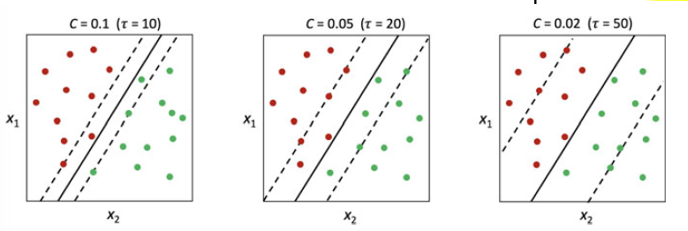
The penalization parameter \(C\) is equal to \(\frac{1}{\tau}\). It has a central role in classification performance. When \(C\) is larger, it produce tighter margins, When \(C\) is smaller, it produce wider margins. It is a trade-off between prediction variance and prediction bias.
Non-Separable Classes
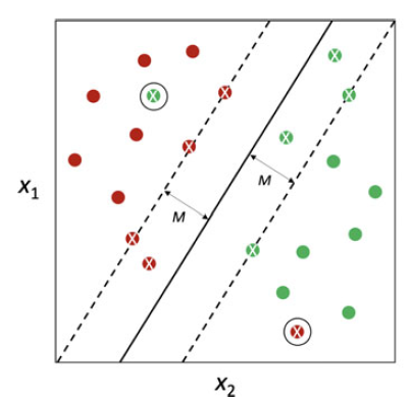
If classes is non separable, a maximal margin hyperplane able to perfectly separate them simply does not exist. If classes are not separable, we would like to allow an observations to cross the boundaries provided by the marginal hyperplanes. Possibly allow for misclassification.
Solution: Provide larger robustness to specific configurations of the observations. Improving classification accuracy for the training observations.
There are 2 approaches to deal with non-separable class in the SVM:
- Feature polynomial expansion
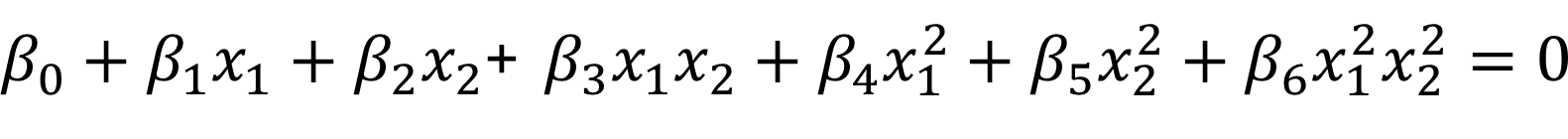
- SVM with kernel adaptation
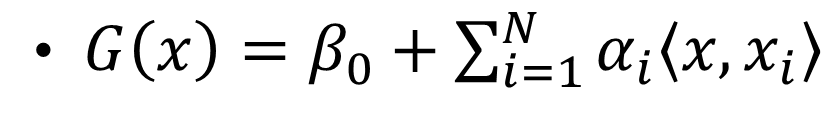
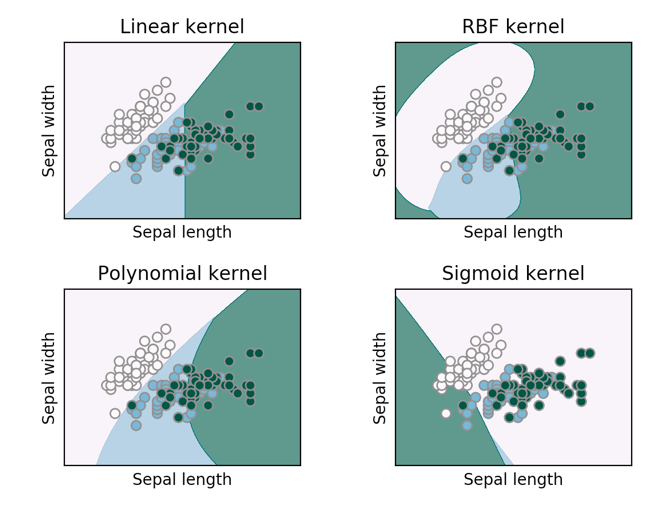
Kernels
SVM utilises kernel functions to map the input data points into a higher dimensional space where the separation between the two classes becomes easier. This allows SVM to solve complex non-linear problem as well.
The SVM’s optimization for kernels:
where 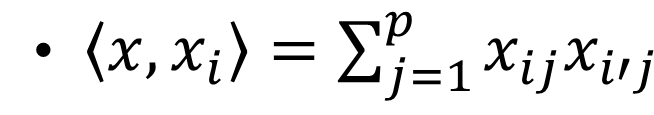 is the inner product between vector \(x\) and \(x_{i}\) and \(\alpha_{i}\) is a parameter specific to every observation \(i=1,2,3,...,N\) .
is the inner product between vector \(x\) and \(x_{i}\) and \(\alpha_{i}\) is a parameter specific to every observation \(i=1,2,3,...,N\) .
The \(<x, x_{i}>\) can be generalize to the nonlinear transformation using kernel transformation as follows:
\[
G(x)= \beta_{0}+\sum\alpha_{i}K(x,x_{i})
\]
where \(K(.)\) is kernel function.
There are two kernel transformation are generally used:
Polynomial kernel
\[
K(x,x_{i})=[1+\sum X_{ij} x_{i'j}]^d
\]
where \(d=1\) equivalent to linear support vector classifier.
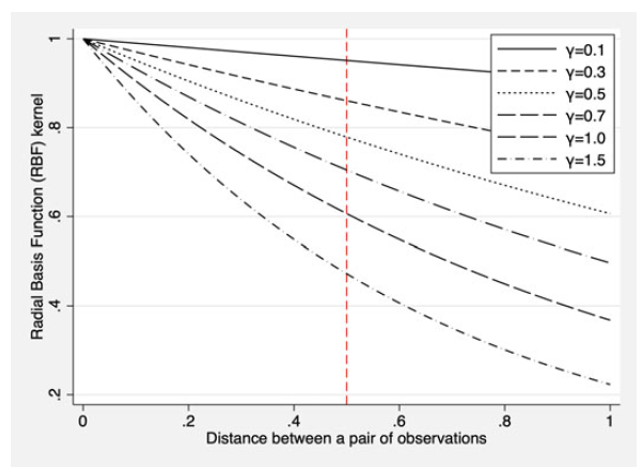
Radial basis kernel
\[
K(x,x_{i})=exp[-\gamma\sum(x_{ij}-x_{i'j})^2]
\]
it is a function of the Euclidean distance between the pair \(i\) and \(i'\) instead of the inner product.
The radial basis kernel behave similar to KNN (k-Nearest Neighbor) classifier. Choosing the right \(\gamma\) implying the sensitiveness of the classification. When \(\gamma\) is low, the classification becomes more sensitive to the distance, and larger distances can count a lot for the classification of a given test point. When \(\gamma\) is high, the classification become less sensitive to the distance and larger distances can count much less for classification (~ small \(k\) in \(k\)NN).
Advantages of SVM
Training is relatively easy
no local minima
It scales relatively well to high dimensional data
Trade-off between classifier complexity and error can be controlled explicitly via \(C\)
Robustness of the results
The “curse of dimensionality” is avoided.
Disadvantages of SVM
Regularization parameter \(C\) that controls the trade-off between maximizing the margin and minimizing the classification error.
A smaller value of \(C\) allows for a wider margin and more misclassifications.
A larger value of \(C\) penalizes misclassifications more heavily, leading to a narrower margin.
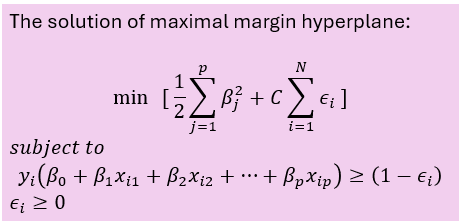
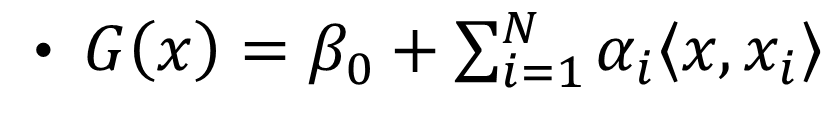
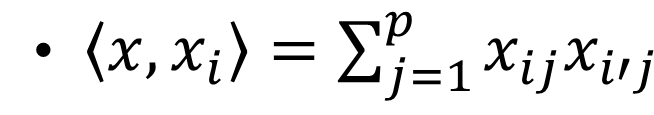 is the inner product between vector
is the inner product between vector